www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Bahas Soal Matematika » Matriks ›
Diketahui \( B = \begin{bmatrix} 2 & 0 \\ 0 & 1 \end{bmatrix} \) dan \( B + C = \begin{bmatrix} 2 & 1 \\ -3 & 1 \end{bmatrix} \). Jika A adalah matriks berukuran 2 x 2 sehingga \( AB + AC = \begin{bmatrix} 4 & 2 \\ -3 & 1 \end{bmatrix} \), maka determinan dari AB adalah…
- 4
- 2
- 1
- -1
- -2
(UTBK 2019)
Pembahasan:
Kita cari matriks \(C\) terlebih dahulu, yakni:
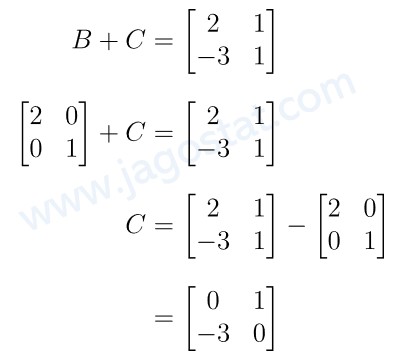
Sekarang, misalkan \( A = \begin{bmatrix} a & b \\ c & d \end{bmatrix} \) sehingga

Selanjutnya, kita cari nilai a, b, c, dan d. Dari hasil di atas diperoleh hubungan berikut:
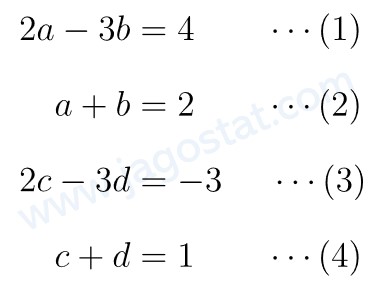
Dari persamaan (1) dan (2) diperoleh nilai a = 2 dan b = 0. Dari persamaan (3) dan (4) diperoleh nilai c = 0 dan d = 1. Jadi, matriks \(A = \begin{bmatrix} a & b \\ c & d \end{bmatrix} = \begin{bmatrix} 2 & 0 \\ 0 & 1 \end{bmatrix} \).
Dengan demikian, determinan matriks AB, yaitu:
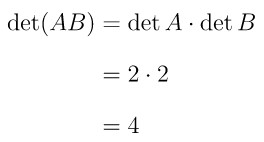
Jawaban A.